Optimization guides for GPUs discuss in length the importance of contiguous ("coalesced", etc.) memory access for achieving high memory bandwidth (e.g. this parallel4all blog post). But how does strided memory access compare across different architectures? Is this something specific to NVIDIA GPUs? Let's shed some light on these questions by some benchmarks.

Why should we care about strided memory access at all? Object-oriented programming teaches us to pack common properties into the same class. Each instantiated object then carries its properties around. An exemplary C++ class for an apple is the following (for simplicity only data members are shown):

  struct apple
  {
    double location[3];
    double weight;
    double temperature;
    int    worms;
    // many more data members
  };

If you now model an apple tree, you will most likely hold an array of objects of type apple. So far so good.

As apples grow, their weight increases. If you want to adjust the weight data member, you will likely write code similar to the following to increase the weight by 10 percent:

  for (int i=0; i<num_apples; ++i)
    apples_array[i].weight *= 1.1;

This is a prototypical example of strided memory access, because the weight data members of two different apple objects are not adjacent in memory.

The perfect hardware architecture provides full memory bandwidth irrespective of the stride of array access. Realistically, we can only hope that memory bandwidth does not drop too quickly as the distance of data members in memory grows. I set up implementations in CUDA, OpenCL, and OpenMP of the strided array access loop

  for (int i=0; i<N; ++i)
    x[i*stride] = y[i*stride] + z[i*stride]

for single precision floating point (float, 32-bit) arrays x, y, and z. The same results will be obtained for 32-bit integers, because memory access is transparent with respect to the interpretation of the bit pattern. Although not tested explicitly, 64-bit data like long integers or double precision floating point numbers result in similar results. The number of array elements was set to one million for GPUs and five million for CPUs and MIC. The latter was necessary to ensure that the whole data set does not fit in cache (and thus report unrealistically high bandwidth).

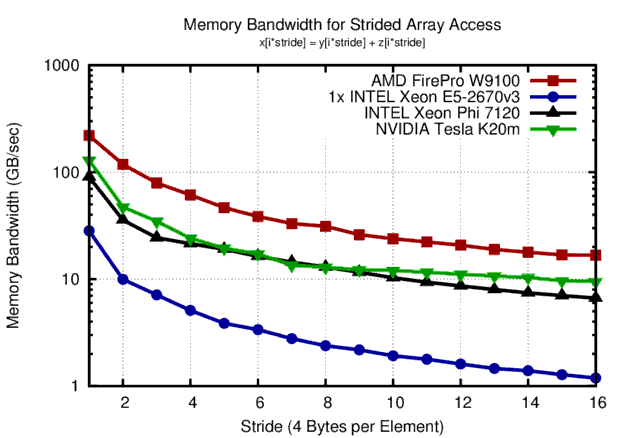
Memory bandwidth obtained for accessing float arrays with different strides. Highest bandwidth is obtained for unit stride, higher strides quickly cause effective bandwidth to decline.

Overall, all four hardware platforms show the exact same qualitative behavior: Unit stride is absolutely preferred. Strides of more than 10 elements (i.e. 40 bytes) result in an order of magnitude smaller bandwidth and should thus be avoided whenever possible.

Furthermore, the benchmark results strongly argue in favor of structure-of-array datastructures instead of array-of-structures. The example of apples on an apple tree modeled by an array of apple objects represents an array-of-structures datastructure. If, however, the apple tree is modeled as

  struct apple_tree
  {
    double *locations[3];
    double *weight;
    double *temperature;
    int    *worms;
    // many more data members
  };

where each of the pointers represents an array, the weight array could be updated at peak memory bandwidth.

Strided memory accesses are not always easy to see. Many times the strided memory access may not be performance-critical. Nonetheless, data layout in memory matters a lot more than second-order effects such as Fortran-vs-C or CUDA-vs-OpenCL. Keep that in mind when coding 🙂

Additional Material

Download files for benchmarking strided memory access with CUDA, OpenCL, or OpenMP.

This blog post is for calendar week 6 of my weekly blogging series for 2016.